Reed-Solomon(RS)은 RAID에서 주로 사용되는 알고리즘입니다. 정확하게는 RAID6에서 사용됩니다.
하둡은 이 RS알고리즘을 가지고 Erasure Coding(EC)을 구현해 냈습니다. 기존의 Replication 방식은 너무나 많은 저장공간을 요구하기 때문에 RS 알고리즘을 기반으로한 EC를 통해 같은 수준의 fault tolerance를 유지하면서 저장공간의 효율성을 달성하고자하는 목적에서였습니다.
EC는 HDFS에 저장되는 파일을 N개의 블록으로 나누고 그 블록들을 RS 알고리즘을 통해 M개의 패리티 블록을 생성합니다. 그리고 이를 통해 Fault tolerance를 확보하게 되죠.
지난 포스팅에서 Parity에 대한 이야기는 XOR 알고리즘에 대한 이야기였습니다. 그래서 XOR 알고리즘으로 어떻게 fault tolerance를 확보하는지는 알고있습니다. 그런데 아직 RS로 어떻게 패리티 블록이 만들어지고 fault tolerance를 확보하는 지는 모르죠.
그럼 RS는 어떤방식으로 작동하고 Parity를 통해 fault tolerance를 가질 수 있는 걸까요?
RS 알고리즘은 인코딩 행렬을 만들고 데이터 행렬을 곱하여 코딩된 데이터를 만듭니다. 이 과정이 인코딩이라고 불립니다. 그리고 역행렬을 통해서 원본 데이터 행렬를 구할 수 있는데 이 과정을 디코딩이라고 합니다.
이를 하나씩 좀 더 상세하게 알아보도록 하죠.
인코딩(Encoding)
우선 인코딩 과정부터 간단한 예를 통해 알아보도록하죠. 여기서는 RS(4, 2) 즉, 4개의 블록과 2개의 패리티 블록을 리드솔로몬 알고리즘으로 만드는 예시를 사용할 겁니다.
RS를 사용하려면 데이터를 행렬에 넣어야합니다. 행렬의 각 요소는 1Byte에 해당합니다.
밑의 그림은 16byte의 파일에 바이트 마다 A~P라는 알파벳으로 네이밍해서 데이터 행렬을 만든 경우입니다.

여기서 중요한 건 데이터의 행렬의 행은 블록입니다. RS(4, 2)에 따라서 4개의 블록을 생성한 것이죠.
- Block 1 :
A B C D - Block 2 :
E F G H - Block 3 :
I J K L - Block 4 :
M N O P
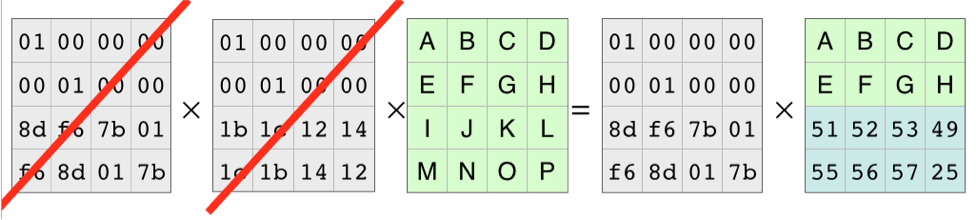
RS는 주어진 데이터행렬을 가지고 인코딩된 데이터(원본 데이터 블록 + 패리티 블록)를 만들기 위해 인코딩 행렬(Encoding metrix)라는 걸 생성합니다. 아래 그림에서 가장 왼쪽에 있는 행렬이 이에 해당합니다.
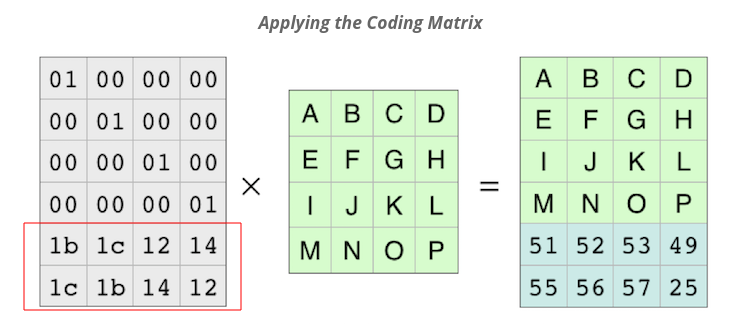
인코딩행렬을 보면 형태가 단위행렬에 두개의 행이 더 추가된 형태입니다. 이는 최종적으로 인코딩된 데이터를 만들때 원본데이터를 그대로 가져오기 위함입니다. 오른쪽에보면 데이터 행렬과 같은 모양이 나타난 것을 볼 수 있죠.
인코딩 행렬의 빨간색 박스가 쳐진 두 행은 패리티 블록을 생성하기 위해 존재합니다. 어떤 값이 들어가지는 지는 알 필요가 없습니다. 그저 인코딩 행렬에는 필요한 패리티 블록을 생성하기 위한 행이 데이터 행렬의 단위행렬에 추가로 붙는다는 것이 중요합니다.
단, 이 행은 필요한 패리티 블록의 수만큼 추가됩니다. 이 예시에서는 RS(4,2)에 따라 2개의 행이 추가로 붙어 6x4행렬을 만들어 냈습니다.
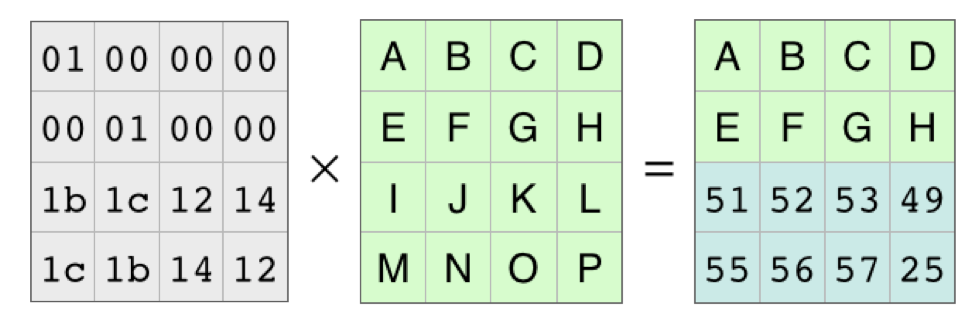
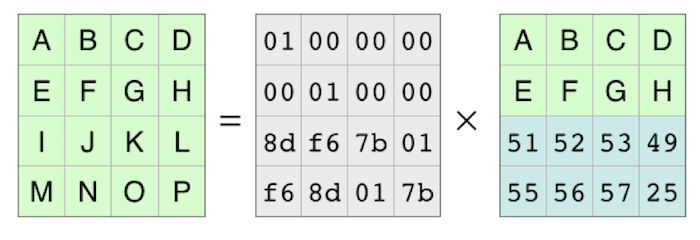
이제 인코딩행렬과 데이터 행렬의 곱연산을 하여 최종적으로 인코딩된 행렬을 구할 수 있습니다. 인코딩된 행렬은 데이터 행렬에 패리티 블록 두개가 붙은 형태입니다. 즉, 데이터 블록 4개와 패리티 블록 2개가 생겨난 것이죠.
- Data block
- Block 1 :
A B C D - Block 2 :
E F G H - Block 3 :
I J K L - Block 4 :
M N O P
- Block 1 :
- Parity block
- Parity block 1 :
51 52 53 49 - Parity block 2 :
55 56 57 25
- Parity block 1 :
디코딩(Decoding)
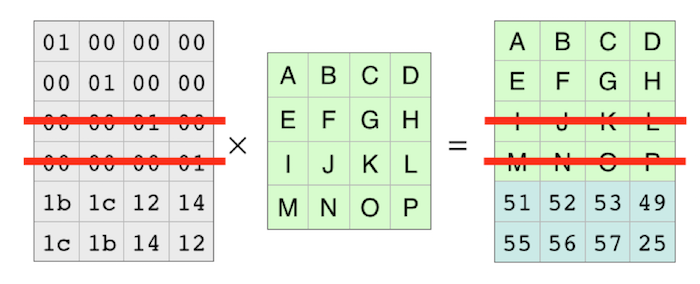
각 블록들은 독립이기 때문에 각 행도 독립적입니다. 따라서 두 개의 행을 지울 수 있습니다. 이는 두개의 블록이 유실된 상황을 의미합니다.
이제 디코딩 행렬을 만들어보죠.
디코딩 행렬은 인코딩 행렬을 가져와서 누락된 블록의 행을 지운 다음 역행렬을 구하면 됩니다.
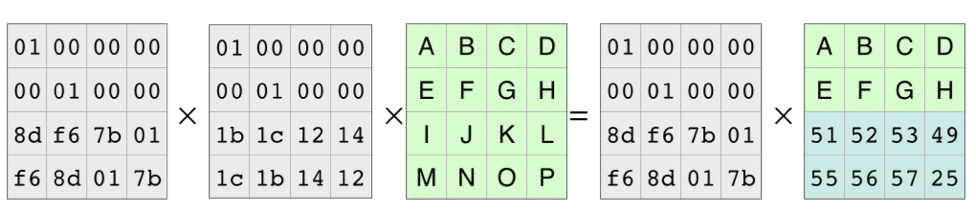
그런 다음 역행렬과 두 행이 삭제된 인코딩된 데이터 행렬의 곱연산을 통해 원본 데이터 행렬을 구할 수 있습니다. 이를 통해 어떤 데이터가 유실됬는지 파악할 수 있고 복구도 할 수 있게 됩니다.
여기서 주목해야할건 2개의 블록이 유실되도 복구가 가능하다는 점입니다.
앞서서 RS(4, 2)를 사용한다고 했던걸 기억하면, 생성하고자하는 패리티 블록의 개수만큼 블록이 손상되도 복구가 가능합니다.
따라서 RS(4, 2)의 fault tolerance는 2입니다. 같은 논리로 RS(6, 3)은 3, RS(10, 4)는 4가 되는 것이죠.
Summary
결국 중요한 건 두가지입니다.
- RS 알고리즘에서 생성하고자하는 패리티 블록의 개수만큼 fault tolerance를 갖는다.
- 보다시피 단순 replication에 비해 인코딩/디코딩 과정은 많은 CPU 연산이 필요하다.
- 다만, 하둡에서는 Intel이 제공한 ISA-L 코더 때문에 어느 정도 해결이 가능하다.